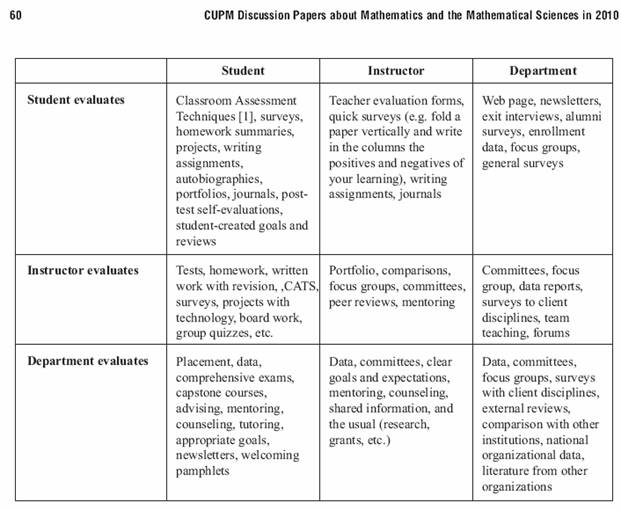
Assessment
Notes
Here are a
few useful links in regards to assessment in Mathematics.
The MAA guidelines for departments
Especially see Appendix A on QL skills
What
quantitative literacy requirements should be established for all students who
receive a bachelor's degree? Over the years, the Mathematical Association of
America (MAA) has approached this question in various ways, most recently by
establishing, in 1989, a Subcommittee on Quantitative Literacy Requirements
(henceforth called the Subcommittee) of its Committee on the Undergraduate
Program in Mathematics. The work of the Subcommittee has been similar in some
respects to the efforts of the National Council of Teachers of Mathematics
(NCTM) that led to its celebrated Curriculum and Evaluation Standards for
School Mathematics (1989) and related publications. The recommendations from
the Subcommittee can be considered to complement those in the Standards. They
also should be viewed as a reasonable extension of a Standards-based high
school experience to the undergraduate level.
The
Subcommittee began with the perception, supported by many recent studies and
reports, that general mathematical knowledge among the American people is in a
sorry state. It assumed that colleges and universities would welcome some
suggestions on what they might do about the situation.
The
discussions and investigations conducted by the Subcommittee led to four
primary conclusions. The conclusions embody a vision that goes well beyond
present practice in most places.
Conclusion
1. Colleges and universities should treat quantitative literacy as a thoroughly
legitimate and even necessary goal for baccalaureate graduates.
Conclusion
2. Colleges and universities should expect every college graduate to be able to
apply simple mathematical methods to the solution of real-world problems.
Conclusion
3. Colleges and universities should devise and establish quantitative literacy
programs each consisting of foundation experience and a continuation
experience, and mathematics departments should provide leadership in the
development of such programs.
Conclusion
4. Colleges and Universities should accept responsibility for overseeing their
quantitative literacy programs through regular assessments.
Supporting Assessment in Undergraduate
Mathematics (SAUM)
The MAA has been serious in promoting assessment in undergraduate mathematics.
Several case studies linked to this report are worth examining.
Arapahoe CC used a common final already in place and tied questions on the
final to benchmarks in the course and performance on that final to
pedagogy. Using the BC cycle, they plan
to use performance on the final to improve pedagogy and thus learning. (See http://www.maa.org/SAUM/cases/johnson-berg-heddens1105-saum.pdf)
Allegheny College examined their Intermediate Algebra course to see if it was
meeting the needs of students. They examined performance on subsequent courses
by students who placed into and took IA and students who placed into and did
not take IA. They also interviewed client departments and students. Their
findings indicated that it was of little value to many students and did not
meet the needs of specific programs. Their findings led to more options for
students – rather than an algebra-intensive course. (See http://www.maa.org/SAUM/cases/harrell-lakins1105-saum.pdf)
Cloud County CC has seen a shift to the vast majority of students having to
take developmental classes, and then college algebra. Their assessment reviewed the contents of
their developmental courses and then the format of college algebra. They found that courses that met longer
(rather than one-hour a day) met with greater long term success. College
Algebra was offered in three different formats and the results on tests and
then on the common exam were compared. (See
http://www.maa.org/SAUM/cases/warkentin-whisler1105-saum.pdf )
The MAA subcommittee on
Assessment promotes a five-phase assessment design:
1) articulation of goals and objectives,
2) development of strategies for reaching goals and objectives,
3) selecting instruments to evaluate the attainment of goals and objectives,
4) gathering, analyzing and interpreting data to determine the extent to which
goals and objectives have been reached, and
5) using the results of assessment for program improvement.
When the final phase is reached, the assessment cycle begins again. This conceptualization of the assessment
process is consistent with other literature on assessment and is applicable at
classroom, departmental or university level.
Assessment
of Student Learning for Improving the Undergraduate Major in Mathematics,
Mathematical Association of America, Subcommittee on Assessment, Committee on
Undergraduate Program Mathematics, 1995.
Steen, L, "Assessing
Assessment," in Gold, B., Keith, S.Z., and Marion, W., eds., Assessment
Practices in Undergraduate Mathematics, 1999, pp. 1-6.
Assessment Standards for School
Mathematics, National Council of Teachers of Mathematics (NCTM), Reston,
Virginia, 1995.
Moskal,
B. "An Assessment Model for the Mathematics Classroom," Mathematics
Teaching in the Middle School, 6 (3), 2000, pp. 192-194.
Beyond CROSSROADS,
AMATYC, Memphis, TN, 2005
Lynn Steen suggests
that we “ask the right questions!”
Inferring that many times in assessment we (in mathematics) do not. Here are a few questions Lynn encourages us
to ask:
• Do students in introductory mathematics
courses learn a balanced sample of important mathematical tools?
• Do these students gain the kind of experience in modeling and communication
skills needed to succeed in other disciplines?
• Do they develop the kind of balance between computational skills and
conceptual understanding appropriate for their long-term needs?
• Why can’t more mathematics problems employ units and realistic measurements
that reflect typical contexts?
• Do students learn to use mathematics in interdisciplinary or “real-world”
settings?
• Are students encouraged (better still,
required) to engage mathematics actively in ways other than through routine
problem sets?
• Do mathematics courses leave students
feeling empowered, informed, and responsible for using mathematics as a tool in
their lives?
• Do program offerings reveal the breadth and interconnections of the
mathematical sciences?
• Do introductory mathematics courses contain
tools and concepts that are important for all students’ intended majors?
• Can students who complete mathematics
courses use what they have learned effectively in other subjects?
• Do students learn to comprehend
mathematically-rich texts and to communicate clearly both in writing and
orally?
Lynn closes with: “Rarely does one find faculty begging
administrators to support assessment programs. For all the reasons cited above,
and more, faculty generally believe in their own judgments more than in the
results of external exams or structured assessments. So the process by which
assessment takes root on campus is more often more top down than bottom
up.” (See
http://www.maa.org/SAUM/cases/steen1105-saum.pdf)
Curriculum Foundation
Reports – The 20 or so reports that make up the vision were created after
considerable discussion with partner disciplines.
Emphasize problem solving skills.
• Develop the fundamental computational skills the partner disciplines require, but emphasize integrative skills: the ability to apply a variety of approaches to single problems, to apply familiar techniques in novel settings, and to devise multi-stage approaches in complex situations.
Emphasize mathematical modeling.
• Expect students to create, solve, and interpret mathematical models.
• Provide opportunities for students to describe their results in several ways: analytically, graphically, numerically, and verbally.
• Use models from the partner disciplines: students need to see mathematics in context.
Emphasize communication skills.
• Incorporate development of reading, writing, speaking, and listening skills into courses.
• Require students to explain mathematical concepts and logical arguments in words. Require them to explain the meaning — the hows and whys — of their results.
Emphasize balance between perspectives.
• Continuous and discrete
• Linear and non-linear
• Deterministic and stochastic
• Deductive and inductive
• Exact and approximate
• Pure and applied
• Local and global
• Quantitative and qualitative
Use a variety of teaching methods since different students have different learning styles. In particular, encourage the use of active learning, including
• in-class problem solving opportunities
• class and group discussions
• collaborative group work, and
• out-of-class projects.
Emphasize the use of appropriate technology.
Emphasize the use of appropriate assessment.
The important relationship between assessment and student learning was discussed extensively at the workshops; i.e., how and what you assess directly affects how and what students learn. Because assessment can be difficult, time-consuming, and tedious, instructors often put less thought and effort into this aspect of course design. However, since effective assessment is critical to learning, instructors must invest in the development of a variety of assessment strategies to measure achievement of course objectives.
WYTIWYG (“What you test is what you get”) was adopted at the final Curriculum Foundations Conference as a central message about assessment. For example, discussions focused on the need for conceptual questions on examinations as opposed to only algorithmic computations and problems that can be solved mechanically with a calculator. It underscores the importance assigned by colleagues in partner disciplines to the development of conceptual understanding.
Indicators of Quality
Undergraduate Mathematics Education
This
NSF-funded project was designed to develop statistical measures (Indicators)
that might be useful to help mathematics departments monitor the quality of
their mathematics courses in the first two years.
The full report looks at the department,
classroom and student. Regarding the classroom, the key issues and indicators
are
àUse interactive
teaching strategies
Indicators: 1.
Instructors use a variety of interactive teaching strategies.
2. Instructors promote active engagement with
mathematics
content.
àUse technology
effectively and appropriately
Indicators: 1. Classrooms must be equipped for using
technology in
instruction.
2. Technology is used in teaching a variety of
mathematics
courses
àInstructors use a variety of assessment methods routinely
Indicators: 1. Instructors seek student feedback to monitor
progress
2. Instructors use a variety of criteria in
determining final
grades.
3. Instructors assess core student proficiencies
using common
items.
In arranging experiences teachers must concentrate on the
important mathematics. What and how we
teach must reflect what is important and how it is
important. Recall the image of the residue. The procedural and conceptual
knowledge that remains is a result of what is learned and how it is learned.
Therefore, what and how we teach must also be reflected in what and how we
assess. Classroom assessment serves several purposes in the learning
environment. Assessment should provide feedback at several levels. First,
assessment provides feedback to the student. It also provides feedback to both
the instructor and the program. Finally, assessment can be used for evaluation
purposes to assign a value to the work. In any case, all assessment instruments
should focus on the important mathematics and require demonstration of
procedural and conceptual understanding that reflects how the mathematics was
experienced. The important mathematics is that which is critical to the
objectives of the course. How the mathematics was experienced dictates how the
assessment should be designed. For example, few inferences about knowledge can
be made if classroom activities stress purely theoretical or procedural
approaches and then the assessment requires modeling and problem solving, or
vice versa. An assessment plan designed to provide inferences about student
knowledge should include a variety of instruments. Examples of instruments
include quizzes, exams, applied or interdisciplinary projects, problem solving
activities, essays, journals and problem sets. These instruments should include
a variety of requirement types addressing both procedural and conceptual
knowledge. These types may include fill in, short answer, calculations,
graphical analysis, numerical analysis, explanations and modeling. Assessment
instruments can be done both in- and out-of-class and should
appropriately integrate technology. In order to most accurately infer student
understanding, assessments must include a variety of problem types and
presentations
Kathleen Snook (USMA):
I recall a visiting professor in my department once saying, “Knowledge is the
residue that remains after the facts are forgotten.”1 This phrase comes to mind often as I
think about teaching and learning. I visualize a glass container or vase filled
with a liquid substance. The substance is made up of many different ingredients
whose individual identities have been lost by being soaked or dissolved in the
liquid. This filled vessel perhaps represents information in a student’s mind
toward the end of the semester, integrated and coherent. After a summer or
semester break the liquid seems to evaporate leaving a residue on the inside
walls of the vase. As educators we must concerned ourselves with the content
and quality of the “residue that remains.” If the appropriate residue remains,
when this knowledge is again needed students can add liquid, shake, and
reconstitute the original mixture.